Principal Components Analysis (PCA)

---

Lecture

2023-10-11

Overview

Today

1. Overview

2. Practical Tips

3. More

4. Wrapup

Dimension Reduction

1. High-dimensional data is hard to visualize and interpret
2. Redundant or irrelevant dimensions in analysis
3. Computational challenges in high dimensions
4. Identify meaningful patterns in data

Climate Data

• Indexed by location, time (and sometimes more)
• A common matrix representation:
  • Each location (grid cell / point) is a column
  • Time is a row
  • Often very high dimensional
  • Strong spatial correlation

PCA

• \(n\) observations, \(p\) features: \(X_1, X_2, \ldots, X_p\)
• find a low-dimensional represnetation that represents as much variation as possible
• the first principal component is the linear combination of features that maximizes the variance
  • \(Z_1 = \phi_{11}X_1 + \phi_{21}X_2 + \ldots + \phi_{p1}X_p\)
  • normalized: \(\sum_{j=1}^p \phi_{j1}^2 = 1\)
• loading: \(\phi_1 = (\phi_{11}, \phi_{21}, \ldots, \phi_{p1})^T\)

Geometric interpretation

The loading vector \(\phi_1\) defines a direction in feature space along which the data vary the most

Principal components analysis (PCA) scores and vectors for climate, soil, topography, and land cover variables. Sites are colored by estimated baseflow yield, and the percent of variance explained by each axis is indicated in the axis titles.

DOI: 10.1016/j.ejrh.2015.04.008

PCA as optimization I

Consider representing the data \(X = (X_1, X_2, \ldots, X_p)\) as a linear model \[ f(Z) = \mu + \phi_q Z \] where:

• \(\mu\) is a location vector.
• \(\phi_q\) is a \(p \times q\) matrix with \(q\) orthogonal unit vectors as columns.
• \(Z\) is a \(q\)-dimensional vector of loadings (or coefficients).

PCA as optimization II

Minimize the reconstruction error: \[ \min \sum_{i=1}^n \| X_i - \phi_q Z \|_2^2 \] assuming \(\mu = 0\) (centered data – more later)

PCA as SVD

We can write the solution as a singular value decomposition (SVD) of the empirical covariance matrix. This reference explains things quite straightforwardly.

Since we are using the covariance matrix, we are implicitly assuming that variance is a good way to measure variability

When might this be a poor assumption?

Uniqueness

Each principal component loading vector is unique, up to a sign flip.

Interpretation

Because we often use space-time data in climate science, we can interpret the principal components as spatial patterns and time series:

1. \(Z\) are the “EOFs” or “principal components”
   1. Dominant spatial patterns
2. \(\phi\): the loading
   1. Time series for each EOF
   2. Reconstruct the data at time \(t\) from the EOFs

Practical Tips

Today

1. Overview

2. Practical Tips

3. More

4. Wrapup

Preprocessing

• Variables should have mean zero (more soon)
• Optional: standardize variables to have unit variance (more later)

Climate anomalies

It is common in climate science to deconstruct a time series into a mean and anomalies: \[ x(t) = \overline{x}(t) + x'(t) \] where \(\overline{x}(t)\) is the climatology and \(x'(t)\) is the anomaly. Typically, this is defined at each location separately.

Computing anomalies

How to define the climatology? Common approaches include:

1. The time-mean (over some reference period)
2. The time-mean, computed separately for each month or season (e.g. DJF, MAM, JJA, SON)
3. A time-mean with a more complicated seasonal cycle removed (eg, sin and cos terms)

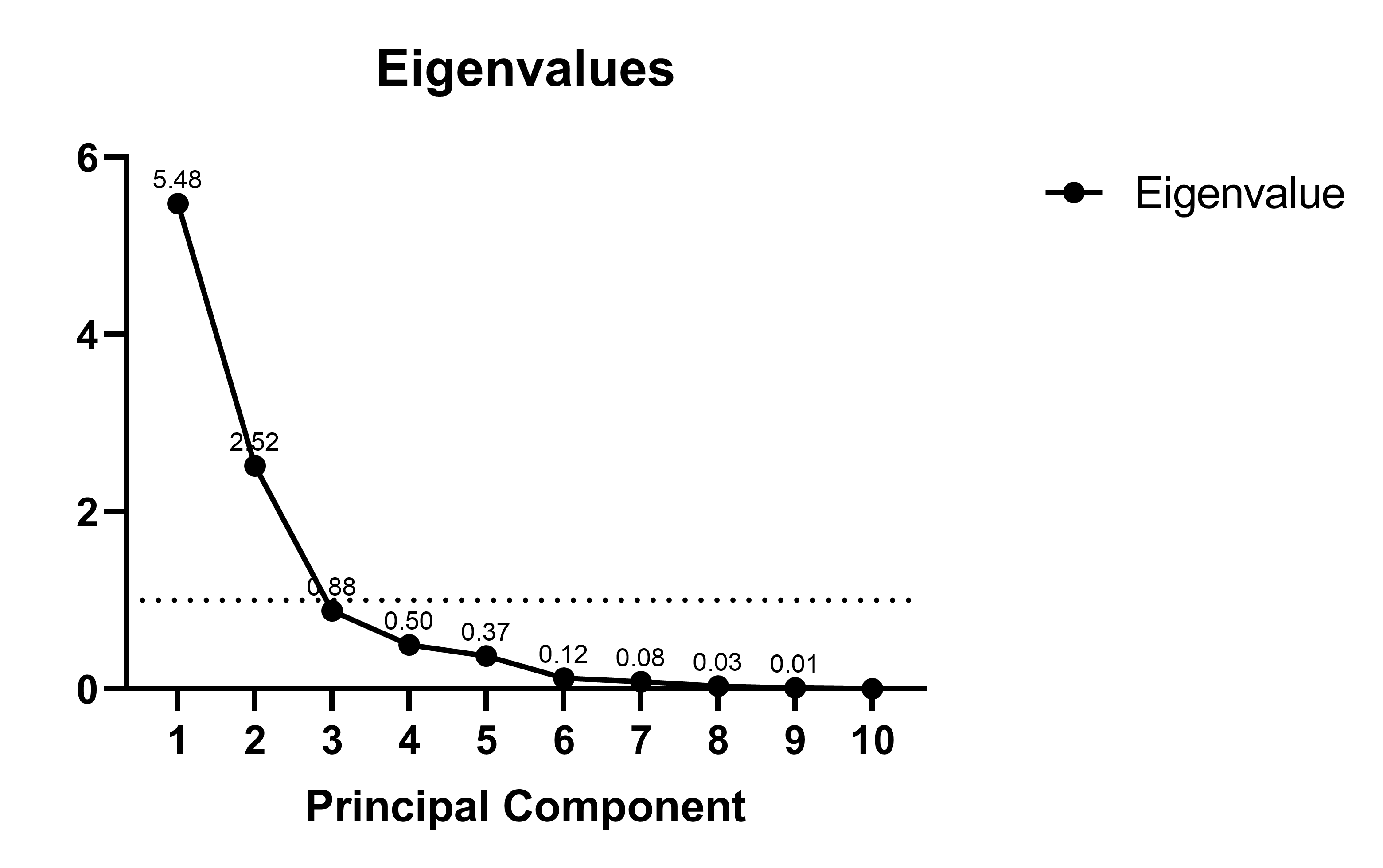
How Many PCs to Use?

• Ideally: use a scree plot (R) to find a natural break
• Practical considerations
• Other heuristics

GraphPad

PCA with Spatial Data

• Centering: variance is the average squared deviation from the mean. Centered and non-centered data will have identical covariance matrices
• Weights: sometimes we have a reason to give one variable more weight than another
  • \(\sqrt{\cos(\phi)}\), where \(\phi\) is latitude. Assigns a standard deviation proportional to the area, which scales with \(\cos \phi\).
  • Sometimes variables are weighted by the inverse of their variances. This is equivalent to standardizing each variable to have unit variance before applying PCA.

Packages for PCA in Julia

• EmpiricalOrthogonalFunctions.jl
  • Based on EOFS in python
• MultivariateStats.jl

More

Today

1. Overview

2. Practical Tips

3. More

4. Wrapup

Examples

• This example uses the Python EOFs library
• Here’s another example of

Beyond PCA

• Probabilistic PCA – going through this may help you understand PCA better
• Robust PCA
• Sparse PCA
• Canonical Correlation Analysis

Wrapup

Today

1. Overview

2. Practical Tips

3. More

4. Wrapup

Summary

PCA is a versatile tool for dimensionality reduction, data visualization, and compression. By understanding its underlying principles and practical applications, we can effectively analyze and interpret complex datasets.

Further reading

• SVD Mathematical Overview is a YouTube video by Steven Brunton that provides a conceptual overview of SVD, which is a linear algebra path to PCA. Note that he defines \(X\) as a matrix of column vectors, whereas we have defined it as a matrix of row vectors (ie, it’s transposed). You’ll want Video 2.
• MIT Computational Thinking Lecture
• Chapter 10.2 of James et al. (2013)
• NCAR Quick Tutorial
• GeoStatsGuy Notebook

References

James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning (Vol. 103). New York, NY: Springer New York.